Program ilustruje powstawanie obrazu w przedstawionym na rysunku zwierciadle kulistym wypukłym o ogniskowej f = -1m. Pozioma biała linia reprezentuje główną oś optyczną zwierciadła, na której zaznaczony jest środek krzywizny zwierciadła O oraz jego pozorne ognisko F. Przedmiotem jest czerwona strzałka znajdująca się w odległości x od zwierciadła. Możemy ją przesuwać przeciągając za pomocą myszki lub klikając w  miejscu, w którym chcemy by się znalazła. Szare linie reprezentują promienie światła wychodzące z końca strzałki-przedmiotu, biegnące w kierunku zwierciadła i odbijające się od jego powierzchni. Trzy z nich wyróżnione są kolorem żółtym. Są to promienie, których bieg łatwo jest wyznaczyć. Promienie te pozwalają na konstrukcyjne znalezienie położenia i wielkości obrazu. Jeden z tych promieni biegnie równolegle do głównej osi optycznej zwierciadła. Po odbiciu się od jego powierzchni porusza się tak jakby wychodził z ogniska F. Kolejny skierowany jest w kierunku ogniska F i dlatego po odbiciu biegnie równolegle do głównej osi zwierciadła. Trzeci, poruszający się w kierunku środka krzywizny O, pada na zwierciadło prostopadle do jego powierzchni. Po odbiciu biegnie więc "z powrotem" po tym samym torze. Przedłużenia (poza powierzchnię zwierciadła) odbitych od zwierciadła trzech wymienionych wyżej promieni oznaczone są na zielono. Punkt ich przecięcia wyznacza miejsce powstania obrazu wierzchołka strzałki (odbite od zwierciadła promienie, które wyszły z wierzchołka strzałki-przedmiotu zachowują się tak, jakby wychodziły z punktu przecięcia się ich przedłużeń, obraz jest obrazem pozornym). Podobnie można wyznaczyć miejsce powstania obrazu każdego punktu przedmiotu. Obraz powstaje w odległości y od zwierciadła.
   Wartości x, y oraz f spełniają równanie zwierciadła:
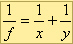Ujemna wartość y oznacza, że obraz powstał za zwierciadłem i jest obrazem pozornym.

Program pochodzi ze zbioru Interactive Physics and Math with Java
Autorzy: © Sergey Kiselev and Tanya Yanovsky-Kiselev
© Polskie tłumaczenie i opis: Marek Godlewski, 15.12.2001r.
    Wydawnictwo ZamKor, Kraków