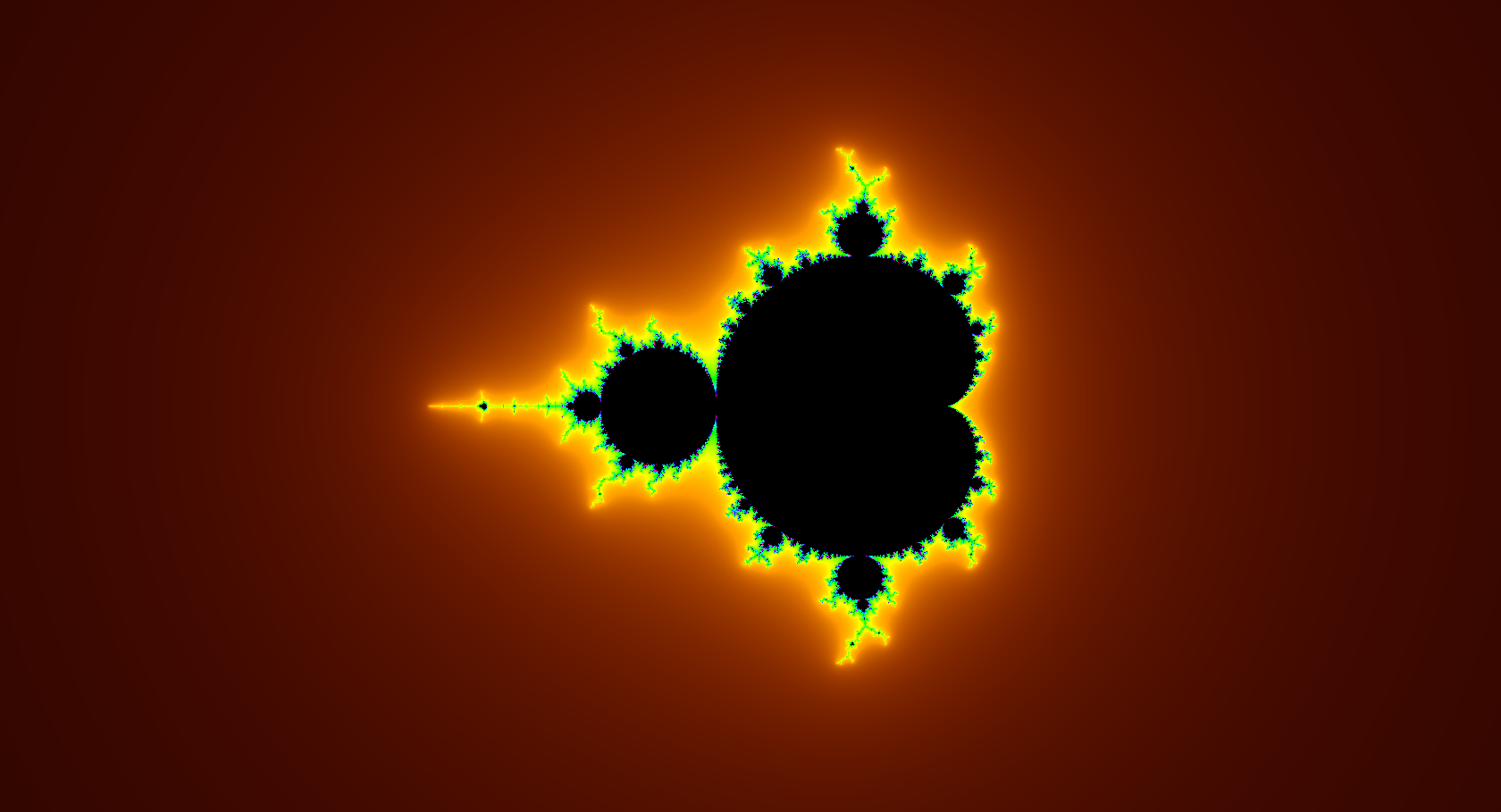Wygenerowany na zajęciach frkatal -Żuk Mandelbrot'aOd najmłodszych lat zadawaliśmy sobie pytania o słuszność ludzkiej nauki w stosunku do skali złożoności świata przyrody. Czy kiedykolwiek uda się nam za pomocą prostych linii i odcinków, kółek i stożków opisać w jakikolwiek sposób znany nam świat przyrody? A jeśli nie, to po co nam te wszystkie lekcje matematyki, fizyki czy astronomii? A może tylko zabieraliśmy się do tego wszystkiego nie z tej strony? Podchodząc do ludzkiej wiedzy holistycznie postanowiliśmy na zajęciach sekcji zasięgnąć języka jakie są możliwości współczesnego naukowca by opisać i zrozumieć złożony Wszechświat. I tak poznaliśmy Żuki Mandelbrota … i jeszcze wiele innych wspaniałych rzeczy.
Fraktale obiły się o uszy prawie każdemu. Ale niewielu nawet dzisiaj wie, że te drzwi dopiero się otwierają. Aby przez nie przejść trzeba posiąść wiedzę w szerokim zakresie. Dlatego zdecydowanie cieszymy się, że matematyka wróciła do ławek matury, a kształcenie przyrodnicze i techniczne nabiera ponownie kolorów. Choć jak powiedział jeden z laureatów Medalu Fieldsa mistrzostwo w swojej dziedzinie uzyskuje się nie wcześniej jak po 10 latach intensywnej pracy. I to bez względu czy zajmujemy się rzutem oszczepem, matematyką czy gra na skrzypcach. Co wymaga od nas cierpliwości i zdeterminowania, by działania nasze przyniosły należyte efekty. Na naszych spotkaniach trudno nauczyć się wszystkiego co jest nam konieczne do dalszego rozwoju w określonych kierunkach. Ale możemy zdobyć inspirację do pracy nad nami samymi. I tak jest tym razem.
Aby zrozumieć elementarne znaczenia jakie towarzysza fraktalom posłużyliśmy się jedynym jak na razie filmem o Fraktalach i tajemnicach przyrody. Fraktale są bowiem tworem matematycznym. Ale jak pokazał już sam ich twórca, wspaniale oddają świat przyrody a nawet więcej. Pozwalają nam zrozumieć dręczące nas odwieczne pytanie: Dlaczego otaczający nas świat jest taki jaki jest?
Fraktal spiralnyDefinicja fraktali może wydać się … dziwna: Fraktal (łac. fractus – złamany, cząstkowy, ułamkowy) w znaczeniu potocznym oznacza zwykle obiekt samo-podobny (tzn. taki, którego części są podobne do całości) albo "nieskończenie subtelny" (ukazujący subtelne detale nawet w wielokrotnym powiększeniu). Ze względu na olbrzymią różnorodność przykładów matematycy obecnie unikają podawania ścisłej definicji i proponują określać fraktal jako zbiór, który posiada wszystkie poniższe charakterystyki albo przynajmniej ich większość. Ich historia jest znacznie starsza niż znane nam współczesne opracowania. Pojęcie fraktala zostało wprowadzone do matematyki przez francuskiego informatyka i matematyka polskiego pochodzenia Benoîta Mandelbrota w latach siedemdziesiątych XX wieku. Odkryty przez niego zbiór Mandelbrota nie był jednak pierwszym przykładem fraktala. Wcześniej istniała już cała gama zbiorów o niecałkowitym wymiarze Hausdorffa, postrzeganych jednak głównie jako kontrprzykłady pewnych twierdzeń. Bardziej systematycznie fraktalami zajmowała się geometryczna teoria miary, mająca swoje początki w pracach Constantina Carathéodory'ego i Felixa Hausdorffa.
Ale aby zrozumieć sens fraktali warto by było przeczytać na początek „BENOÎT B MANDELBROT - FRAKTALNA GEOMETRIA NATURY”. Zdobycie tej pozycji na naszym runku jest co najmniej trudne. Ale za pewne warte zachodu. Zdobędziemy wiedzę u samego źródła.
Nasze spotkanie z fraktalami pozwoliło nam zrozumieć jak istotna jest wiedza ścisła do poznania naszego świata. To co wydawało się nieuchwytne, zmiany ciśnienia krwi, zawiłość gałęzi drzew czy choćby struktura naszego układu krwionośnego, niespodziewanie daje się uchwycić, opisać i obliczyć. Ponownie matematyka pokazała, że nie jest abstrakcją, ale wymagającą od nas forma rzeczywistości. Aby z niej korzystać trzeba się uczyć, pracować i doskonalić siebie w wielu dziedzinach. Mandelbrot wykazał się niezwykłym geniuszem pokazując biskość matematyki fraktali i świata przyrody. Dzięki temu lekarze, astronomowie, przyrodnicy zrozumieli jak można wykorzystać tę wiedze do opisu i zrozumienia świata w ich dziedzinie pracy i badań. Nagle okazało się, że zrozumienie funkcjonowania dżungli amazońskiej i jej wpływu na klimat na ziemi jest możliwy. Dostaliśmy narzędzie dające szansę leczenia raka poprzez jego wykrycie we wczesnym stadium. Astronomowie zdobyli możliwość zrozumienia natury zjawisk w kosmosie, których do tej pory nie mogli zrozumieć. Astronomia to w zasadzie jedyna nauka, która nie ma możliwości dotknięcia swoich obiektów badań. Nie dość, że są dalekie, to często są skrajnie niebezpieczne dla badacza. Nawet artyści skorzystali na udomowieniu fraktali.
W ramach naszego spotkania spróbowaliśmy wygenerować swój fraktal dzięki dostępnym narzędziom w sieci. Fraktale to jednak nie tylko obrazy, choć sam autor matematyki fraktali zdecydowanie był za obrazowaniem wiedzy o nich niż stworzeniem abstrakcyjnej wiedzy. Dzisiaj każdy kto coś wie lub słyszał o fraktalach kojarzy je z niezwykłymi rysunkami i obrazami. Sens jednak tego jest taki, że dopiero wiedza matematyczna daje nam możliwości samodzielnego zgłębienia zastosowań jakie dla nich znajdziemy. Stąd zadanie na wakacje, a będzie ich cała lista, to poznanie wiedzy o liczbach zespolonych i wygenerowanie swojego fraktala. Można to zrobić na kartce papieru albo za pomocą komputera. Ważna jest wyjątkowość swojej pracy. Może powstanie z tego jakaś matematyczna wystawa?
Przeczytaj więcej: 
Definicja fraktali może wydać się … dziwna: Fraktal (łac. fractus – złamany, cząstkowy, ułamkowy) w znaczeniu potocznym oznacza zwykle obiekt samo-podobny (tzn. taki, którego części są podobne do całości) albo "nieskończenie subtelny" (ukazujący subtelne detale nawet w wielokrotnym powiększeniu). Ze względu na olbrzymią różnorodność przykładów matematycy obecnie unikają podawania ścisłej definicji i proponują określać fraktal jako zbiór, który posiada wszystkie poniższe charakterystyki albo przynajmniej ich większość. Ich historia jest znacznie starsza niż znane nam współczesne opracowania. Pojęcie fraktala zostało wprowadzone do matematyki przez francuskiego informatyka i matematyka polskiego pochodzenia Benoîta Mandelbrota w latach siedemdziesiątych XX wieku. Odkryty przez niego zbiór Mandelbrota nie był jednak pierwszym przykładem fraktala. Wcześniej istniała już cała gama zbiorów o niecałkowitym wymiarze Hausdorffa, postrzeganych jednak głównie jako kontrprzykłady pewnych twierdzeń. Bardziej systematycznie fraktalami zajmowała się geometryczna teoria miary, mająca swoje początki w pracach Constantina Carathéodory'ego i Felixa Hausdorffa.
